|
reorrido
-
-
Cambio horizontal entre dos puntos de una línea. Es igual a la diferencia entre las abscisas de los dos puntos dados. La relación de elevación a recorrido da el gradiente (o pendiente) del segmento de línea que pasa a través de los dos puntos dados.
-
Sistema de referencia
Un sistema de referencia o marco de referencia es un conjunto de convenciones usadas por un observador para poder medir laposición y otras magnitudes físicas de un sistema físico y de mecanica. Las trayectorias medidas y el valor numérico de muchas magnitudes son relativas al sistema de referencia que se considere, por esa razón, se dice que el movimiento es relativo. Sin embargo, aunque los valores numéricos de las magnitudes pueden diferir de un sistema a otro, siempre están relacionados por relaciones matemáticas tales que permiten a un observador predecir los valores obtenidos por otro observador.
En mecánica clásica frecuentemente se usa el término para referirse a un sistema de coordenadas ortogonales para el espacio euclídeo (dados dos sistemas de coordenadas de ese tipo, existe un giro y una traslación que relacionan las medidas de esos dos sistemas de coordenadas).
Foco (geometría)
En geometría, el foco de una curva o de una superficie es un punto singular, por lo general no perteneciente a ella, respecto del cual se mantienen constantes determinadas distancias relacionadas con todos los puntos de la misma. Una figura puede tener asociados más de un foco.
Foco de una circunferencia
El foco de la circunferencia es su centro. Respecto del mismo, todos los puntos se encuentran a la misma distancia.
Focos de una elipse
Los focos de la elipse son dos puntos. Respecto de ellos la suma de las distancias a cualquier otro punto de la elipse es constante.
Foco de una parábola
El foco de la parábola es un punto. Respecto del foco, cada punto de la parábola posee la misma distancia que hasta una recta llamadadirectriz.
-
 cuando la parábola va hacia la derecha; cuando la parábola va hacia la derecha;
-
 cuando la parábola va hacia la izquierda. cuando la parábola va hacia la izquierda.
formula f(c,o)
Focos de una hipérbola
Los focos de la hipérbola son dos puntos. Respecto de ellos, permanecen constante la diferencia de distancias (en valor absoluto) a cualquier punto de dicha hipérbola.
Directriz
Una directriz se dice de aquello que marca las condiciones en que se genera algo.1
En geometría la directriz es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea, superficie o volumen (que se llama generatriz).2
Si la directriz es una línea recta, y la generatriz es otra línea recta que gira en torno a ella, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es curva genera esferas, elipsoides, etc. Si la generatriz se desplaza sobre una o más directrices, genera una superficie reglada.
La directriz puede ser una línea curva, por ejemplo, una circunferencia generatriz que rueda sobre otra circunferencia, tangencialmente. Un punto vinculado a ella describe una trayectoria curva que se denomina ruleta cicloidal.
Generatriz
La generatriz1 es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.2
Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una curva, genera esferas,elipsoides, etc. Si se desplaza sobre una o más directrices, genera una superficie reglada.
La generatriz puede ser una línea curva, por ejemplo, una circunferencia que rueda sobre otra circunferencia directriz, tangencialmente. Un punto vinculado a ella describe una trayectoria curva que se denomina ruleta cicloidal.
Lado recto
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.
Concavidad
la concavidad de una curva o de una superficie es la parte que se asemeja a la zona interior de una circunferencia o de una esfera,1 es decir, que tiene su parte hundida dirigida al observador
Simetría
es un rasgo característico de formas geométricas, sistemas, ecuaciones y otros objetos materiales, o entidades abstractas, relacionada con su invariancia bajo ciertas transformaciones, movimientos o intercambios
Simetría esférica
La simetría esférica es la simetría respecto a un punto central, de modo que un sistema físico o geométrico tiene simetría esférica cuando todos los puntos a una cierta distancia del punto central son equivalentes.
Simetría reflectiva
La simetría reflectiva (a veces llamada simetría bilateral o simetría especular) se reconoce fácilmente, porque una mitad es el reflejo de la otra.
Parábola
En matemáticas, una parábola (del griego παραβολή) es la sección cónica resultante de cortar un cono recto con un plano cuyo ángulo de inclinación respecto al eje de revolución del cono sea igual al presentado por su generatriz. El plano resultará por lo tanto paralelo a dicha recta.nota 1 nota 2 Se define también como el lugar geométrico de los puntos de un plano que equidistan de una recta llamada directriz,nota 3 y un punto exterior a ella llamado foco. En geometría proyectiva, la parábola se define como la curva envolvente de las rectas que unen pares de puntos homólogos en unaproyectividad semejante o semejanza.
La parábola aparece en muchas ramas de las ciencias aplicadas debido a que su forma se corresponde con las gráficas de las ecuaciones cuadráticas. Por ejemplo, son parábolas las trayectorias ideales de los cuerpos que se mueven bajo la influencia exclusiva de la gravedad (vermovimiento parabólico y trayectoria balística).
Valor absoluto
En matemática, el valor absoluto o módulo1 de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de 3 y de -3.
El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.
Movimiento parabólico
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme.
Puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
Movimiento rectilíneo uniforme
Un movimiento es rectilíneo cuando el móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.
- Movimiento que se realiza sobre una línea recta.
- Velocidad constante; implica magnitud y dirección constantes.
- La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
-
Velocidad
-
La velocidad es una magnitud física de carácter vectorial que expresa el desplazamiento de un objeto por unidad de tiempo. Se representa por 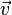 o o 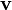 . Sus dimensiones son [L]/[T]. Su unidad en el Sistema Internacional es el m/s. . Sus dimensiones son [L]/[T]. Su unidad en el Sistema Internacional es el m/s.
En virtud de su carácter vectorial, para definir la velocidad deben considerarse la dirección del desplazamiento y el módulo, el cual se denomina celeridad o rapide
Movimiento rectilíneo uniformemente acelerado
-
El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un móvil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.
También puede definirse el movimiento como el que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.
Caída libre
-
En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídasreales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o asatélites no propulsados en órbita alrededor de la Tierra. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en elespacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni deparacaídas durante un cierto trayecto.
Coordenadas geográficas
- Las coordenadas geográficas son un sistema de referencia que utiliza las dos coordenadas angulares, latitud (Norte y Sur) y longitud (Este y Oeste) y sirve para determinar los ángulos laterales de la superficie terrestre (o en general de uncírculo o un esferoide). Estas dos coordenadas angulares medidas desde el centro de la Tierra son de un sistema decoordenadas esféricas que están alineadas con su eje de un sistema de coordenadas geográficas incluye un datum, meridiano principal y unidad angular. Estas coordenadas se suelen expresar en grados sexagesimales:
-
Análisis matemático
-
El análisis es una rama de la ciencia matemática que estudia los números reales, los complejos y construcciones derivadas a partir de ellos, así como las funciones entre esos conjuntos y construcciones derivadas. Se empieza a desarrollar a partir del inicio de la formulación rigurosa del cálculo y estudia conceptos como la continuidad, la integración y la diferenciabilidad de diversas formas.
Una de las diferencias entre el álgebra y el análisis es que en este segundo recurre a construcciones que involucran sucesiones de un número infinito de elementos, mientras que álgebra usualmente es finitista.
-
Cálculo infinitesimal
-
El cálculo infinitesimal o cálculo de infinitesimales constituye una parte muy importante de la matemática moderna. Es normal en el contexto matemático, por simplificación, simplemente llamarlo cálculo.
El cálculo, como algoritmo desarrollado en el campo de la matemática, incluye el estudio de los límites, derivadas, integrales y series infinitas, y constituye una gran parte de la educación de las universidades modernas. Más concretamente, el cálculo infinitesimal es el estudio del cambio, en la misma manera que la geometría es el estudio del espacio.
El cálculo infinitesimal tiene amplias aplicaciones en la ciencia y la ingeniería y se usa para resolver problemas para los cuales el álgebra por sí sola es insuficiente. Este cálculo se construye con base en el álgebra, la trigonometría y la geometría analítica e incluye dos campos principales, cálculo diferencial y cálculo integral, que están relacionados por el teorema fundamental del cálculo. En matemática más avanzada, el cálculo es usualmente llamado análisis y está definido como el estudio de las funciones.
-
Diferencial de una función
-
Este artículo habla sobre la definición tradicional del diferencial, para otros usos dentro de la matemática vea diferencial (cálculo, desambiguación), para usos más generales vea diferencial (desambiguación)
En cálculo infinitesimal, el diferencial de una función es un objeto matemático que representa una linealización de una función y = ƒ(x) con respecto a cambios en la variable independiente. Formalmente el diferencial de una función  es una 1-forma, definida por la expresión: es una 1-forma, definida por la expresión:

Para funciones de una variable la expresión anterior puede escribirse simplemente como:
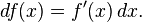
Aproximación lineal
En matemáticas, una aproximación lineal es una aproximación de una función cualquiera usando una transformación lineal. Por ejemplo, dada una función diferenciable f de una variable real, se puede expresar (generalizada en el Teorema de Taylor) de la siguiente manera:
-

donde  es el error. La aproximación se obtiene desechando el error. es el error. La aproximación se obtiene desechando el error.
-

-
Gráfica de una función
En matemáticas, la gráfica de una función:
-

es la representación gráfica de la correspondencia entre los elementos del conjunto dominio y los del conjunto imagen. Es el conjunto formado por todos los pares ordenados (x, f(x)) de la función f; es decir, como un subconjunto del producto cartesiano X×Y.
Las únicas funciones que se pueden trazar de forma completa son las de una sola variable, con un sistema de coordenadas cartesianas, donde cada abscisa representa un valor de la variable del dominio y cada ordenada representa el valor correspondiente del conjunto imagen. Si la función es continua, entonces la gráfica formará una línea recta o curva.
En el caso de funciones de dos variables es posible visualizarlas de forma unívoca mediante una proyección geométrica, pero a partir de tres variables tan solo es posible visualizar cortes (con un plano) de la función para los que los valores de todas las variables, excepto dos, permanezcan constantes.Lo cual es cierto para los valores de x cercanos a a. La expresión derecha es la de la recta tangente a la gráfica de f en a. Por esta razón también se llama aproximación de la recta tangente.
Recta
En geometría euclidiana, la recta o la línea recta, se extienden en una misma dirección, existe en una sola dimensión y contiene infinitospuntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, es decir, no posee principio ni fin.
Es uno de los entes geométricos fundamentales, junto al punto y el plano. Son considerados conceptos apriorísticos ya que su definición sólo es posible a partir de la descripción de las características de otros elementos similares. Así, es posible elaborar definiciones basándose en los postulados característicos que determinan relaciones entre los entes fundamentales. Las rectas se suelen denominar con una letra minúscula.
En geometría analítica las líneas rectas pueden ser expresadas mediante una ecuación del tipo y = m x + b, donde x, y son variables en un plano cartesiano. En dicha expresión m es denominada la "pendiente de la recta" y está relacionada con la inclinación que toma la recta respecto a un par de ejes que definen el plano. Mientras que b es el denominado "término independiente" u "ordenada al origen" y es el valor del punto en el cual la recta corta al eje vertical en el plano.
Ecuación de primer grado
Una ecuación de primer grado o ecuación lineal significa que es un planteamiento de igualdad, involucrando una o más variables a la primera potencia, que no contiene productos entre las variables, es decir, una ecuación que involucra solamente sumas y restas de una variable a laprimera potencia.
Variable
En matemáticas y en lógica, una variable es un símbolo constituyente de un predicado, fórmula o algoritmo. El término «variable» se utiliza aún fuera del ámbito matemático para designar una cantidad susceptible de tomar distintos valores numéricos dentro de un conjunto de números especificado.1
En contraste, una constante es un valor que no cambia (aunque puede no ser conocido, o indeterminado). En este contexto, debe diferenciarse de una constante matemática, que es una magnitud numérica específica, independientemente de la naturaleza del problema dado.
Algoritmo
En matemáticas, lógica, ciencias de la computación y disciplinas relacionadas, un algoritmo (del griego y latín, dixit algorithmus y este a su vez del matemático persa Al-Juarismi1 ) es un conjunto preescrito de instrucciones o reglas bien definidas, ordenadas y finitas que permite realizar una actividad mediante pasos sucesivos que no generen dudas a quien deba realizar dicha actividad.2 Dados un estado inicial y una entrada, siguiendo los pasos sucesivos se llega a un estado final y se obtiene una solución. Los algoritmos son el objeto de estudio de la algoritmia.1
En la vida cotidiana, se emplean algoritmos frecuentemente para resolver problemas. Algunos ejemplos son los manuales de usuario, que muestran algoritmos para usar un aparato, o las instrucciones que recibe un trabajador por parte de su patrón. Algunos ejemplos en matemática son el algoritmo de multiplicación, para calcular el producto, el algoritmo de la división para calcular el cociente de dos números, el algoritmo de Euclides para obtener el máximo común divisor de dos enteros positivos, o el método de Gauss para resolver un sistema lineal de ecuaciones.
Algoritmo de multiplicación
Un algoritmo de multiplicación es un algoritmo (o método) para multiplicar dos números. Dependiendo del tamaño de los números, existen diferentes algoritmos. Los algoritmos de multiplicación existen desde el advenimiento del sistema decimal.
Sistema de numeración decimal
El sistema de numeración decimal, también llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética laspotencias del número diez. El conjunto de símbolos utilizado (sistema de numeración arábiga) se compone de diez cifras diferentes: cero (0); uno (1); dos (2); tres (3); cuatro (4); cinco (5); seis(6); siete (7); ocho (8) y nueve (9).
Excepto en ciertas culturas, es el sistema usado habitualmente en todo el mundo y en todas las áreas que requieren de un sistema de numeración. Sin embargo hay ciertas técnicas, como por ejemplo en la informática, donde se utilizan sistemas de numeración adaptados al método del binario o el hexadecimal.
Base (aritmética)
En un sistema de numeración posicional, se le llama base al número que define el orden de magnitud en que se ve incrementada cada una de las cifras sucesivas que componen el número. Es también la cantidad de símbolos presentes en dicho sistema. Por ejemplo, el sistema de numeración decimal (el más utilizado en la actualidad) utiliza como base el número 10 (diez): hay 10 símbolos o dígitos, y cada uno de ellos se incrementa en un orden de magnitud de 10 por cada posición consecutiva.
Por convención, se denota la base con la cifra 10, independientemente de la base elegida, así, en el sistema de numeración binario, por ejemplo, el 'dos' -que es la base- se escribe 10.
Cancelacion Decimos que hemos cancelado un numero o una expresi ´ on algebraica cuando aplicamos una de las siguientes propiedades de los numeros reales: ´
a + (a) = 0
Ley de los Senos
La ley de los senos se usa para encontrar los ángulos de un triángulo en general. Se se conocen dos lados y el ángulo comprendido entre ellos dos, se puede usar junto con la ley de senos para encontrar el tercer lado y los otros dos ángulos.
Ley de los Cosenos
La ley de los cosenos para el cálculo de uno de los lados de un triángulo cuando se conocen el ángulo opuesto y los otros dos lados. Puede ser utilizado en conjunción con la ley de los senos para encontrar todos los lados y ángulos.
Línea
Una línea es una sucesión continua de puntos trazados, como por ejemplo un trazo o un guion. Las líneas suelen utilizarse en la composición artística, se denomina en cambio «raya» a trazos rectos sueltos, que no forman una figura o forma en particular.1
En matemáticas y geometría, línea suele denotar línea recta o curva
En geometría, la línea también puede considerarse la distancia más corta entre dos puntos puestos en un plano
Hipérbola
Una hipérbola es el lugar geométrico de los puntos de un plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a la distancia entre los vértices, la cual es una constante positiva.
Sección cónica
Se denomina sección cónica (o simplemente cónica) a todas las curvas intersección entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen las cónicas propiamente dichas. Se clasifican en cuatro tipos: elipse, parábola, hipérbola y circunferencia.
Elipse
La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos llamados focos es constante.
Foco de una circunferencia
El foco de la circunferencia es su centro. Respecto del mismo, todos los puntos se encuentran a la misma distancia.
Focos de una elipse
Los focos de la elipse son dos puntos. Respecto de ellos la suma de las distancias a cualquier otro punto de la elipse es constante.
Foco de una parábola
El foco de la parábola es un punto. Respecto del foco, cada punto de la parábola posee la misma distancia que hasta una recta llamadadirectriz.
-
 cuando la parábola va hacia la derecha; cuando la parábola va hacia la derecha;
-
 cuando la parábola va hacia la izquierda. cuando la parábola va hacia la izquierda.
formula f(c,o)
Catenaria
Catenaria es la curva que describe una cadena suspendida por sus extremos, sometida a un campo gravitatorio uniforme. La palabra deriva del latín catenarĭus (propio de la cadena). Por extensión, en matemáticas se denomina catenaria a la curva que adopta una cadena, cuerda o cable ideal perfectamente flexible, con masa distribuida uniformemente por unidad de longitud, suspendida por sus extremos y sometida a la acción de un campo gravitatorio uniforme. La evoluta de la catenaria es la tractriz.
Tractriz
Se denomina tractriz a la curva que describe un objeto (situado en P) que es arrastrado por otro (situado en A), que se mantiene a distancia constanted y que se desplaza en línea recta. Su ecuación en coordenadas cartesianas es:
-
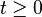
-

-
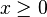
-

-

Poliedro
Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico πολύεδρον (polyedron), de la raíz πολύς (polys), "muchas" y de έδρα (edra), "base", "asiento", "cara".
Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topológicos del concepto en cualquier dimensión. Así, el punto o vértice es el semejante topológico del poliedro en cero dimensiones, una arista o segmento lo es en 1 dimensión, el polígono para 2 dimensiones; y el polícoro el de cuatro dimensiones. Todas estas formas son conocidas como politopos, por lo que podemos definir un poliedro como un polítopo tridimensional
Geometría descriptiva
La geometría descriptiva es un conjunto de técnicas geométricas que permite representar el espacio tridimensional sobre una superficie bidimensional. Por tanto, mediante «lectura» adecuada posibilita resolver problemas espaciales en dos dimensiones de modo que se garantiza la reversibilidad del proceso.
En la época actual se reconocen dos modelos, en los cuales se les considera: 1) «lenguaje» de representación y de sus aplicaciones; 2) tratado de geometría. Aunque no es exactamente lo mismo, su desarrollo ha estado relacionado con el de la Geometría proyectiva.
Geometría proyectiva
Se llama geometría proyectiva a la rama de la matemática que estudia las propiedades de incidencia de las figuras geométricas, pero abstrayéndose totalmente del concepto de medida. A menudo se usa esta palabra también para hablar de la teoría de la proyección llamada geometría descriptiva.
Medición
La medición es un proceso básico de la ciencia que consiste en comparar un patrón seleccionado con el objeto o fenómeno cuya magnitud física se desea medir para ver cuántas veces el patrón está contenido en esa magnitud.1
Ecuación diferencial
Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:
Numerador
El numerador es el número superior de una fracción e indica el numero de partes elegidas.
Fracción
En matemáticas, una fracción, número fraccionario, o quebrado (del vocablo latín frāctus, fractĭo -ōnis, roto, o quebrado)1 es la expresión de una cantidad dividida entre otra cantidad ; es decir que representa un cociente no efectuado de números. Por razones históricas también se les llama fracción común, fracción vulgar o fracción decimal. El conjunto matemático que contiene a las fracciones es el conjunto de los números racionales, denotado  . .
Geometría diferencial
En matemáticas, la geometría diferencial es el estudio de la geometría usando las herramientas del análisis matemático. Los objetos de estudio de este campo son las variedades diferenciables (tal y como la topología diferencial) tanto como las nociones de conexión y curvatura (que no se estudia en la topología diferencial).
Las aplicaciones modernas de la geometría diferencial han dado el estado del arte que goza la física.
Curvatura
En matemáticas, la curvatura se refiere a cualquiera de una serie de conceptos vagamente relacionados en las diferentes áreas de la geometría. Normalmente se refiere a un concepto métricode objetos matemáticos o geométricos. Por extensión también se usa el término para referirse a un número u objeto matemático que caracteriza la forma y magnitud de la curvatura. Más específicamente el término curvatura puede referirse a alguno de estos conceptos:
Radio de curvatura
El radio de curvatura es una magnitud que mide la curvatura de un objeto geométrico tal como una línea curva, una superficie o más en general una variedad diferenciable embebida en unespacio euclídeo.
Variedad de Riemann
En la geometría de Riemann, una variedad de Riemann es una variedad diferenciable real en la que cada espacio tangente se equipa con unproducto interior de manera que varíe suavemente punto a punto. Esto permite que se definan varias nociones métricas como longitud de curvas,ángulos, áreas (o volúmenes), curvatura, gradiente de funciones y divergencia de campos vectoriales.
Espacio tangente
En geometría diferencial, espacio tangente es el conjunto asociado a cada punto de una variedad diferenciable formado por todos los vectores tangentes a dicho punto (véase fig.1). Es un espacio vectorial de la misma dimensión que la dimensión de la variedad.
El conjunto de todos los espacios tangentes, debidamente topologizado, forma el llamado fibrado tangente. Resulta ser en sí mismo otra variedad de dimensión doble de la dimensión de la variedad de entrada.
Espacio vectorial
En álgebra abstracta, un espacio vectorial es una estructura algebraica creada a partir de un conjunto no vacío, una operación interna (llamada suma, definida para los elementos del conjunto) y una operación externa (llamada producto por un escalar, definida entre dicho conjunto y otro conjunto, con estructura de cuerpo ), con 8 propiedades fundamentales.
A los elementos de un espacio vectorial se les llama vectores y a los elementos del cuerpo, escalares.
Estructura algebraica
En álgebra abstracta, una estructura algebraica, también conocida como sistema algebraico,1 es una n-tupla (a1, a2, ..., an), donde a1 es un conjunto dado no vacío, y {a2, ..., an} un conjunto de operaciones aplicables a los elementos de dicho conjunto.
|
 y
y  (los dos extremos de un segmento de recta, por ejemplo) es una recta, llamada mediatriz. Dicho de otra forma, la mediatriz es la recta que se interseca perpendicularmente con un segmento
(los dos extremos de un segmento de recta, por ejemplo) es una recta, llamada mediatriz. Dicho de otra forma, la mediatriz es la recta que se interseca perpendicularmente con un segmento  en su punto medio (
en su punto medio ( ).
). , de los conjuntos
, de los conjuntos 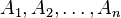 es un subconjunto del producto cartesiano
es un subconjunto del producto cartesiano en este caso se representa
en este caso se representa  como
como  , pudiéndose decir que la relación pertenece a A a la n.
, pudiéndose decir que la relación pertenece a A a la n.
 es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 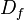 . En
. En  se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío.
se denomina dominio a un conjunto conexo, abierto y cuyo interior no sea vacío. ) incluyen tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes1 (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como:
) incluyen tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes1 (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como:  , el número real log2, cuya trascendencia fue mentada por Euler en el siglo XVIII.2
, el número real log2, cuya trascendencia fue mentada por Euler en el siglo XVIII.2 y
y  de forma que el segundo es extensión del primero, diremos que
de forma que el segundo es extensión del primero, diremos que  es trascendente sobre
es trascendente sobre  si no existe ningún polinomio
si no existe ningún polinomio ![p \in K[x]](https://upload.wikimedia.org/math/3/6/a/36a6013b43f19ae5b9eaea971cbaee30.png) del que
del que  es raíz (
es raíz ( ).
). , en negrita de pizarra) que deriva de «cociente» (Quotienten varios idiomas europeos). Este conjunto de números incluye a los números enteros (
, en negrita de pizarra) que deriva de «cociente» (Quotienten varios idiomas europeos). Este conjunto de números incluye a los números enteros ( ), y es un subconjunto de los números reales (
), y es un subconjunto de los números reales ( ).
). , donde
, donde  y
y  son enteros, con
son enteros, con  diferente de cero y donde esta fracción esirreducible. Es cualquier número real que no es racional.
diferente de cero y donde esta fracción esirreducible. Es cualquier número real que no es racional.





 cuando la parábola va hacia la derecha;
cuando la parábola va hacia la derecha; cuando la parábola va hacia la izquierda.
cuando la parábola va hacia la izquierda.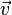 o
o 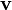 . Sus
. Sus  es una
es una 
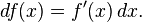

 es el error. La aproximación se obtiene desechando el error.
es el error. La aproximación se obtiene desechando el error.

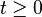

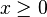


 .
.